Como continuación de la entrada anterior en el blog, que estaba dedicada a las diferentes coordenadas astronómicas, vamos a abordar ahora una forma de representar gráficamente la posición de objetos en la esfera celeste. Cuando se trata de representar en el plano la esfera celeste de forma global se suele utilizar la proyección de Mollweide. En este artículo veremos como generar representaciones gráficas con la proyección de Mollweide utilizando la librería matplotlib de Python. La posibilidad de generar este tipo de representaciones gráficas resulta bastante útil , pero como veremos, es un tanto "tricky".
Autor: Eduardo Martín Calleja
Importaciones y referencias¶
%matplotlib inline
from __future__ import division
import numpy as np
import matplotlib.pyplot as plt
import ephem # para las conversiones de coordenadas
from IPython.core.display import HTML # Para incluir imágenes como HTML
# Generar un cuadro con versiones de las librerías utilizadas en este notebook
#https://github.com/jrjohansson/version_information
%load_ext version_information
%version_information numpy, matplotlib, ephem
Como crear una proyección de Mollweide¶
Vamos a realizar un primer ejemplo de proyección de Mollweide utilizando las librerías numpy y matplotlib de la forma más estandar posible. En el gráfico siguiente vamos a representar tres rectángulos curvilineos con \(\Delta RA=60^\circ\) de base y \(\Delta \delta = 45^\circ\) de altura en tres posiciones diferentes
r = 90
theta = np.arange(0,2*np.pi,0.1)
x = np.array([0,np.pi/3,np.pi/3,0,0])
y = np.array([0,0,np.pi/4,np.pi/4,0])
fig = plt.figure(figsize=(10, 5))
ax = fig.add_subplot(111, projection="mollweide", axisbg ='LightCyan')
ax.grid(True)
ax.plot(x,y)
ax.plot(x+np.pi/6,y+np.pi/6)
ax.plot(x-np.pi/2,y-np.pi/2);
Las lecciones que podemos extraer del anterior ejemplo son las siguientes:
Los valores de x e y , los cuales serán normalmente ascensiones rectas y declinaciones, o bien longitudes y latitudes, ¡deben ser expresados en radianes!, los valores de x e y deben estar en el rango: \(-\pi < x < \pi\) , \(-\pi/2 < y < \pi/2\). Podriamos comprobar que los valores que excedan este rango (por ej. \(x = 3 \pi/2\)) no aparecen en la gráfica.
La escala de los ejes en la representación gráfica cubre respectivamente los intervalos [-180, 180] y [-90, 90], es decir, la representación gráfica traduce los valores en radianes a valores en grados en estos intervalos.
Otro hecho significativo que tendremos que tener en cuenta en las proyecciones astronómicas, es que en la escala horizontal del gráfico generado el sentido positivo es hacia la derecha, mientras que en las representaciones astronómicas la ascensión recta aumenta hacia el Este (situado convencionalmente a la izquierda en los mapas celestes)
La escala horizontal está centrada en x=0, lo cual debe ser tenido en cuenta ya que en las representaciones de la esfera celeste interesa a veces situar el centro en \(RA = 90^\circ\) o en \(RA = 180^\circ\)
Teniendo en cuenta todos estos puntos vamos a escribir a continuación una función que representará un par de arrays de valores (típicamente RA y Dec) en un diagrama de dispersión de puntos en la esfera celeste con la proyección de Mollweide
def plot_mwd(RA,Dec,org=0,title=u'Proyección de Mollweide', projection='mollweide'):
''' RA, Dec son arrays de la misma longitud.
RA toma valores en [0,360), Dec en [-90,90],
los cuales representan ángulos en grados.
org es el origen del gráfico, 0 o multipo de 30, en [0,360)
title el título del gráfico
projection es el tipo de proyección: 'mollweide', 'aitoff', 'hammer', 'lambert'
'''
x = np.remainder(RA+360-org,360) # desplazamos los valores de RA
ind = x>180
x[ind] -=360 # Conversión de escala a [-180, 180]
x=-x # invertir la escala: el Este a la izquierda
tick_labels = np.array([150, 120, 90, 60, 30, 0, 330, 300, 270, 240, 210])
tick_labels = np.remainder(tick_labels+360+org,360)
fig = plt.figure(figsize=(10, 5))
ax = fig.add_subplot(111, projection=projection, axisbg ='LightCyan')
ax.scatter(np.radians(x),np.radians(Dec)) # convertir grados a radianes
ax.set_xticklabels(tick_labels) # Añadimos escala en el eje x
ax.set_title(title)
ax.title.set_fontsize(15)
ax.set_xlabel("RA")
ax.xaxis.label.set_fontsize(12)
ax.set_ylabel("Dec")
ax.yaxis.label.set_fontsize(12)
ax.grid(True)
Vamos a probar la función anterior haciendo una representación centrada en \(RA = 90^\circ\) de unos pocos pares de coordenadas expresadas en grados y comprobando que se representan en la posición adecuada:
coord = np.array([(0,30), (60,-45), (240,15), (150,-75)])
plot_mwd(coord[:,0],coord[:,1], org=90, title = u'Test función plot_mwd')
Finalmente vamos a representar un array de pares de coordenadas generadas de forma aleatoria
np.random.seed(0)
nrand = np.random.rand(100,2) # Array (100,2) de valores aleatorios en [0,1)
nrand *= np.array([360.,180.]) # array de valores en [0,360)x[0,180)
nrand -=np.array([0.,90.]) # array de valores en [0,360)x[-90,90)
nrand = nrand[(-86 < nrand[:,1]) & (nrand[:,1] < 86)] # Evitar Matplotlib Runtime Warning,
# manteneniendonos lejos de las singularidades en -90º y 90º
RA = nrand[:,0]
Dec = nrand[:,1]
plot_mwd(RA,Dec)
A título de curiosidad, preguntemosnos como se vería el plano de nuestra galaxia, es decir, la Via Láctea, en un gráfico de la esfera celeste en coordenadas ecuatoriales RA, Dec
El plano galáctico es el que tiene coordenada de latitud b = 0 en el sistema de coordenadas galácticas. Vamos a generar un array de coordenadas galácticas de latitud 0 y lo convertiremos a coordenadas ecuatoriales con la librería ephem.
lon_array = np.arange(0,360)
lat = 0.
eq_array = np.zeros((360,2))
for lon in lon_array:
ga = ephem.Galactic(np.radians(lon), np.radians(lat))
eq = ephem.Equatorial(ga)
eq_array[lon] = np.degrees(eq.get())
RA = eq_array[:,0]
Dec = eq_array[:,1]
plot_mwd(RA, Dec, 180, title = u'Plano galáctico en coordenadas ecuatoriales \n (Proyección de Mollweide)')
Proyección de Aitoff¶
Otro sistema de proyección con el que nos encontraremos en ocasiones y que es también utilizado en astronomía para representar una visión global de la esfera celeste, es la proyección de Aitoff. Presenta un aspecto similar a la de Mollweide, pero, al contrario de esta, las líneas de igual latitud (paralelos) se representan por líneas curvas, y estas están regularmente espaciadas.
r = 90
theta = np.arange(0,2*np.pi,0.1)
x = np.array([0,np.pi/3,np.pi/3,0,0])
y = np.array([0,0,np.pi/4,np.pi/4,0])
fig = plt.figure(figsize=(10, 5))
ax = fig.add_subplot(111, projection="aitoff", axisbg ='LightCyan')
ax.grid(True)
ax.plot(x,y)
ax.plot(x+np.pi/6,y+np.pi/6)
ax.plot(x-np.pi/2,y-np.pi/2);
Vamos a generar la imagen del plano galáctico en la proyección de Aitoff
lon_array = np.arange(0,360)
lat = 0.
eq_array = np.zeros((360,2))
for lon in lon_array:
ga = ephem.Galactic(np.radians(lon), np.radians(lat))
eq = ephem.Equatorial(ga)
eq_array[lon] = np.degrees(eq.get())
RA = eq_array[:,0]
Dec = eq_array[:,1]
plot_mwd(RA, Dec, 180, title = u'Plano galáctico en coordenadas ecuatoriales \n (Proyección de Aitoff)', projection='aitoff')
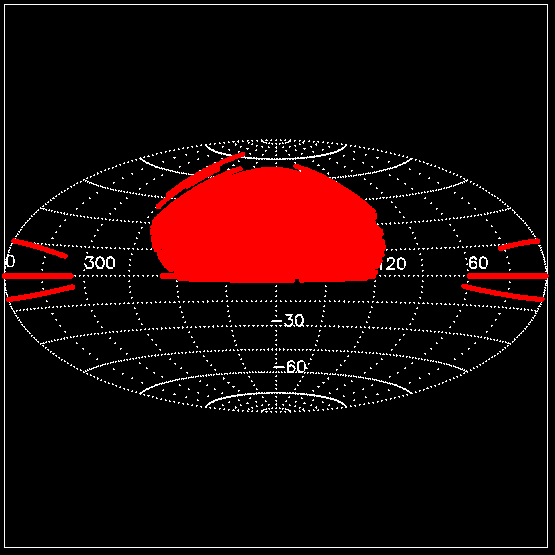
Y como ejemplo de uso de este sistema de proyección, podemos comparar el mapa anterior con el mapa de cobertura de la release DR7 de datos del Sloan Digital Sky Survey (SDSS), que se puede consultar en cobertura DR7 SDSS, el cual se presenta en una proyección de Aitoff centrada en \(RA = 180^\circ\)
HTML('<img src="http://classic.sdss.org/dr7/dr7photo_big.gif" WIDTH=500>')
En esta imagen se aprecia como la encuesta del SDSS evita la zona cercana al plano galáctico, en el cual se concentran la mayoría de las estrellas de nuestra galaxia. Es natural, ya que el objeto principal del SDSS es la fotometría de los objetos extragalácticos.
La proyección de Mollweide conserva las áreas¶
Una propiedad característica de la proyección de Mollweide, que la hace especialmente útil para representar la distribución global de objetos o magnitudes en la esfera celeste y hacerse una idea de su densidad, es que si bien no conserva formas ni ángulos, si conserva las áreas. es decir, áreas iguales en el globo celeste se representan mediante áreas iguales en la proyección de Mollweide. La proyección de Aitoff no tiene esta propiedad.
Para comprobar visualmente este hecho, vamos a representar una serie de rectángulos de igual área. Por rectángulos entenderemos en este caso áreas delimitadas entre dos meridianos y dos parelelos celestes. Vamos a proceder del siguiente modo:
En primer lugar, llamando theta al arco de meridiano que delimita la extensión de un casquete esférico centrado en el polo Norte celeste, utilizaremos el hecho de que el área de dicho casquete es proporcional a 1-cos(theta). Este hecho se deriva de la fórmula de cálculo del área de un casquete esférico, junto con un poco de trigonometría elemental.
Este hecho lo utilizaremos para establecer una serie de valores del ángulo de declinación dec que señalan paralelos tales que el área comprendida entre estos paralelos es la misma en todos los casos (esto implica en particular que los paralelos en cuestión no serán equidistantes)
Finalmente subdividiremos estas áreas en rectángulos delimitados por meridianos espaciados entre sí pi/6 (30 grados). Las regiones rectangulares resultantes tendrán todas el mismo área.
theta_1 = 30./180 * np.pi # 15 grados expresados en radianes
# Creamos un array con valores de theta (ángulo medido desde el polo N)
# Que delimitan regiones entre paralelos celestes de igual área
theta_a = np.zeros(7)
for n in range(0,7):
theta_n = np.arccos(n*np.cos(theta_1)-n+1)
theta_a[n] = theta_n
theta_a
# Los convertimos a valores de declinaciones
# medidas desde el ecuador celeste
dec_a = np.pi/2 - theta_a
dec_a
# Y finalmente representamos 6 regiones rectangulares de igual área
fig = plt.figure(figsize=(10, 5))
ax = fig.add_subplot(111, projection="mollweide", axisbg ='LightCyan')
ax.set_title(u'Ejemplo de áreas iguales \n (proyección de Mollweide)')
ax.grid(True)
for n in range(6):
rec_n = np.array([(n* np.pi/6, dec_a[n+1]),
((n +1) * np.pi/6, dec_a[n+1]),
((n +1) * np.pi/6, dec_a[n]),
(n* np.pi/6, dec_a[n]),
(n* np.pi/6, dec_a[n+1])])
x = rec_n[:,0]
y = rec_n[:,1]
ax.plot(x,y)
En la figura anterior se vé como la altura de los rectángulos en la representación de Mollweide se va estrechando para compensar el aumento de anchura a medida que nos acercamos al ecuador celeste, con el fin de que las áreas de todas las regiones sean identicas entre sí en la representación gráfica, al igual que lo son en la realidad.
No hay comentarios:
Publicar un comentario